Harmonic-plus-Noise

Harmonic-plus-Noise synthesis decomposes an audio signal into two complementary components: harmonic and noise. The harmonic component models periodic sounds as a sum of sinusoidal oscillators, while the noise component captures the non-periodic, broadband content.

A signal $x[n]$ is expressed as:

$ x[n] = e[n] + \sum_{k=1}^N A_k[n] \sin\left(2\pi f_k[n] n T + \phi_k[n]\right) $

Where $T$ is the sampling period, $N$ is the number of harmonics, while $A_k[n]$, $f_k[n]$, and $\phi_k[n]$ are respectively the amplitude, frequency, and phase of the $k$-th harmonic. The noise component $e[n]$ can be modeled using subtractive synthesis:

$ e[n] = \mathcal{F}\big(\mathcal{N}[n]; \Theta\big), $

Where $\mathcal{N}[n]$ is an input noise (e.g., white noise or gaussian noise), $\mathcal{F}$ is a filter function, and $\Theta$ are the parameters of the filter (e.g. cutoff frequency).

DDSP Implementation

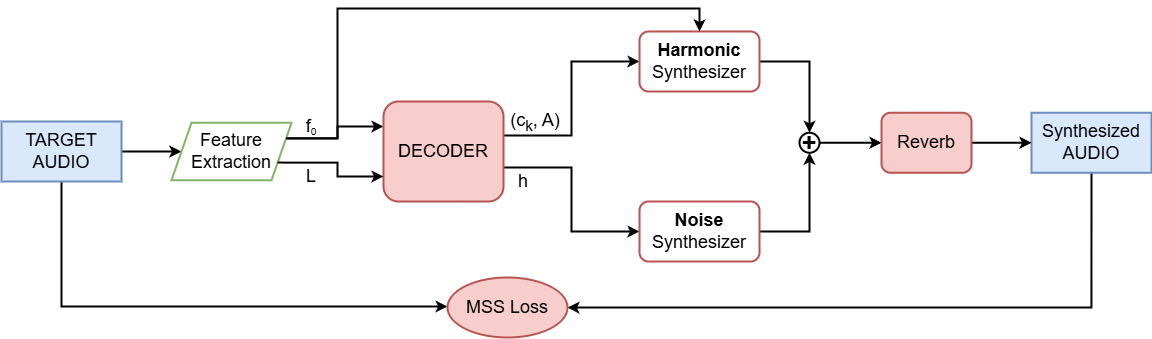The HpN architecture employs a decoder, formed of recurrent and fully connected layers, conditioned on a sequence of pitch ($f_0$) and loudness ($L$) frames to predict the overall amplitude of the audio signal ($A$), the normalized distribution of spectral variations among the various harmonics ($c_k$), and the coefficients of the filter used to model the noise component ($h$).

Audio Examples

	Reference	Anchor (LPC)
🪈 Flute
🎺 Trumpet
🎻 Violin
🎹 Piano

Harmonic-plus-Noise

	Full	Reduced	Reduced+AD	Reduced+CD
🪈 Flute
🎺 Trumpet
🎻 Violin
🎹 Piano